Slowly convergent series
We could replace integer summation $\sum_{i=1}^\infty i$ with the harmonic series, however, the traditional harmonic
series $\sum\limits_{k=1}^\infty{1\over k}$ diverges. It turns out that if we omit the terms whose denominators in
decimal notation contain any digit or string of digits, it converges, albeit very slowly (Schmelzer & Baillie 2008),
e.g.
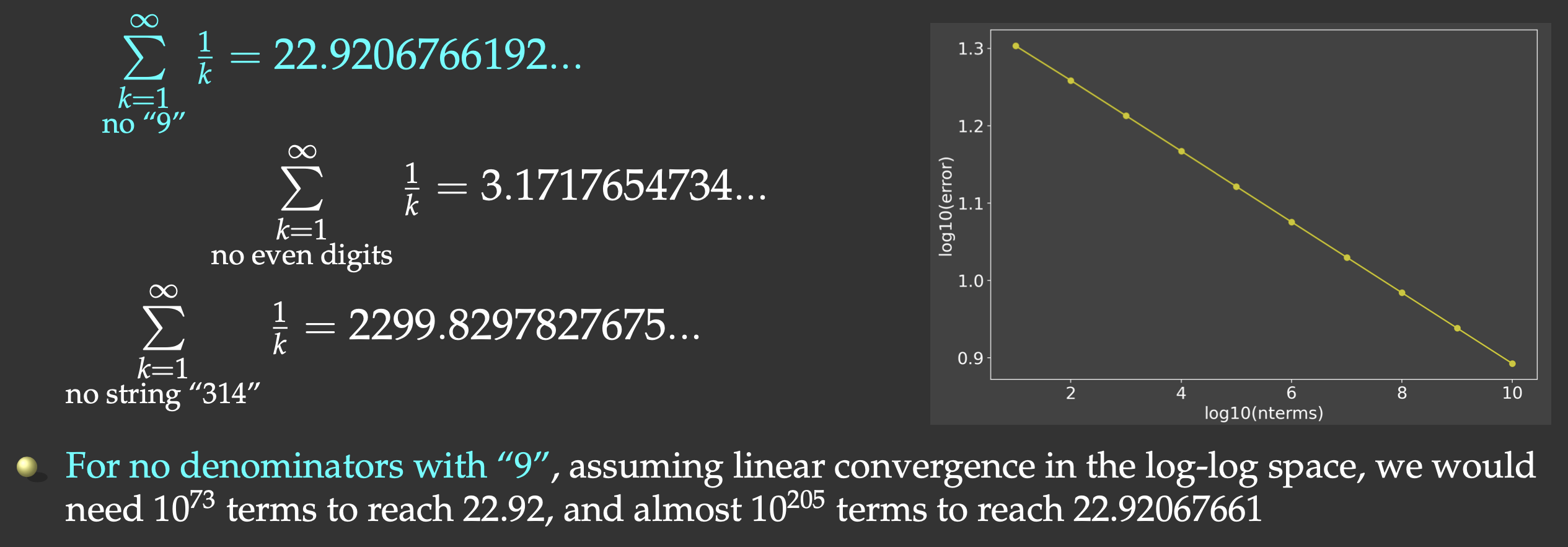
But this slow convergence is actually good for us: our answer will be bounded by the exact result (22.9206766192…) on the upper side. We will sum all the terms whose denominators do not contain the digit “9”.
We will have to check if “9” appears in each term’s index i. One way to do this would be checking for a substring in a
string:
if !occursin("9", string(i))
<add the term>
end
It turns out that integer exclusion is ∼4X faster (thanks to Paul Schrimpf from the Vancouver School of Economics @UBC for this code!):
function digitsin(digits::Int, num) # decimal representation of `digits` has N digits
base = 10
while (digits ÷ base > 0) # `digits ÷ base` is same as `floor(Int, digits/base)`
base *= 10
end
# `base` is now the first Int power of 10 above `digits`, used to pick last N digits from `num`
while num > 0
if (num % base) == digits # last N digits in `num` == digits
return true
end
num ÷= 10 # remove the last digit from `num`
end
return false
end
if !digitsin(9, i)
<add the term>
end
Let’s now do the timing of our serial summation code with 1e9 terms:
function slow(n::Int64, digits::Int)
total = Float64(0) # this time 64-bit is sufficient!
@time for i in 1:n
if !digitsin(digits, i)
total += 1.0 / i
end end
println("total = ", total)
end
slow(10, 9) # precompile the functions `slow()` and `digitsin()`
slow(Int64(1e9), 9) # total = 14.2419130103833, runtime 38.23s 38.13s 38.18s