Parallelizing Julia set

In this section I will describe one of the two projects you can work on this afternoon. The project is the mathematical problem to compute Julia set – no relation to Julia language! A Julia set is defined as a set of points on the complex plane that remain bound under infinite recursive transformation $f(z)$. We will use the traditional form $f(z)=z^2+c$, where $c$ is a complex constant. Here is our algorithm:

1. pick a point $z_0\in\mathbb{C}$
2. compute iterations $z_{i+1}=z_i^2+c$ until $|z_i|>4$ (arbitrary fixed radius; here $c$ is a complex constant)
3. store the iteration number $\xi(z_0)$ at which $z_i$ reaches the circle $|z|=4$
4. limit max iterations at 255
   4.1 if $\xi(z_0)=255$, then $z_0$ is a stable point
   4.2 the quicker a point diverges, the lower its $\xi(z_0)$ is
5. plot $\xi(z_0)$ for all $z_0$ in a rectangular region $-1<=\mathfrak{Re}(z_0)<=1$, $-1<=\mathfrak{Im}(z_0)<=1$

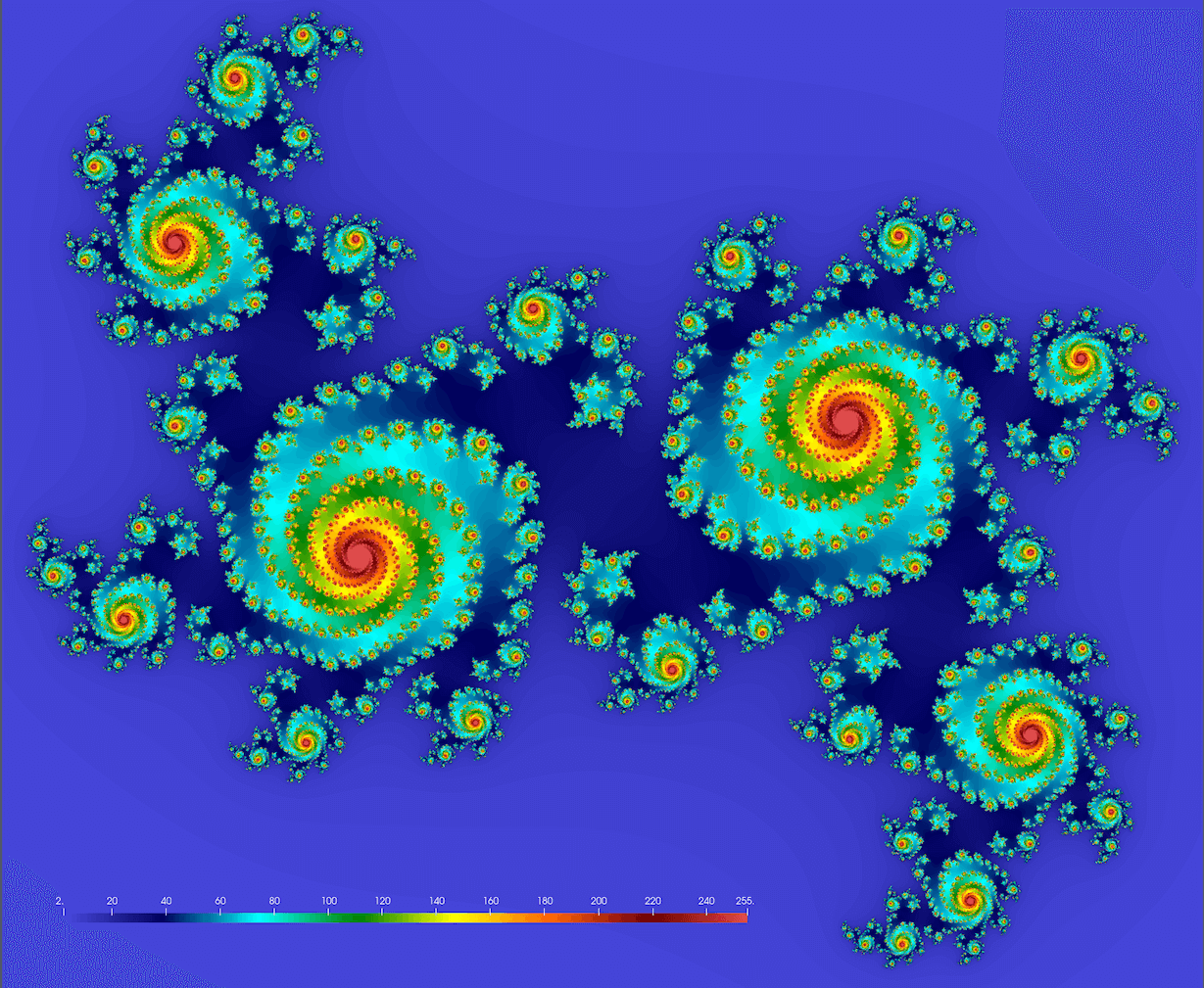
We should get something conceptually similar to this figure (here $c = 0.355 + 0.355i$; we’ll get drastically different fractals for different values of $c$):

Below is the serial code juliaSetSerial.jl. First, you need to install the required packages:

] add ProgressMeter
] add NetCDF

Next, let’s study the code:

using ProgressMeter, NetCDF

function pixel(i, j, width, height, c, zoomOut)
    z = (2*(j-0.5)/width-1)+(2*(i-0.5)/height-1)im   # rescale to -1:1 in the complex plane
    z *= zoomOut
    for i = 1:255
        z = z^2 + c
        if abs(z) >= 4
            return i
        end
    end
    return 255
end

n = Int(8e3)             # plot size
height, width = n, n
c, zoomOut = 0.355 + 0.355im, 1.2

println("Computing Julia set ...")
data = zeros(Float32, height, width);   # local array
@showprogress for i in 1:height, j in 1:width
    data[i,j] = pixel(i, j, width, height, c, zoomOut)
end

# println("Very slow plotting ...")
# using Plots
# gr()    # initialize the gr backend
# file_name = "$(height)x$(width)_$(c.re)_$(c.im)"
# png(heatmap(data, size=(width,height), color=:gist_ncar), file_name)   # save to PNG

# println("On-screen b/w plotting ... slow too")
# using ImageView
# imshow(data)

println("Writing NetCDF ...")
filename = "test.nc"
isfile(filename) && rm(filename)        # compact if statement
nccreate(filename, "stability", "x", collect(1:height), "y",
         collect(1:width), t=NC_FLOAT, mode=NC_NETCDF4, compress=9);
ncwrite(data, filename, "stability");

Let’s run this code. It’ll produce the file test.nc that you can download to your computer and visualize with ParaView or other visualization tool.

Exercise 11

1. Compare the expected and actual file sizes.
2. Try other parameter values:

c, zoomOut = 0.355 + 0.355im, 1.2   # the default one: spirals
c, zoomOut = 1.2exp(1.1π*im), 1     # original textbook example
c, zoomOut = -0.4 - 0.59im, 1.5     # denser spirals
c, zoomOut = 1.34 - 0.45im, 1.8     # beans
c, zoomOut = 0.34 -0.05im, 1.2      # connected spiral boots

3. You can also try increasing problem sizes up from $8000^2$. Will you have enough physical memory for $16000^2$? How does this affect the runtime?

Parallelizing

How would we parallelize this problem? We have a large array, so we can use DistributedArrays and compute it in parallel. Here are the steps:

1. Some functions (packages) should be defined (loaded) on all processes.
2. data array should be distributed.
3. You need fillLocalBlock(data, width, height, c, zoomOut) to compute local pieces of data in parallel. If you don’t know where to start in this project, begin with looking at the complete example with fillLocalBlock() from the previous section.
4. You can replace

@showprogress for i in 1:height, j in 1:width
    data[i,j] = pixel(i, j, width, height, c, zoomOut)

with

data = dzeros(Float32, height, width);   # distributed 2D array of 0's
@time @sync for i in workers()
    @spawnat i fillLocalBlock(data, width, height, c, zoomOut)

5. Why do we need @sync in the previous for block?
6. To the best of my knowledge, NetCDF’s ncwrite() is serial in Julia. Is there a parallel version of NetCDF for Julia? If not, then unfortunately we will have to use serial NetCDF. How do we do this with distributed data?
7. Time only the for loop in computing the array. Is your parallel code faster?

Results

Finally, here are my timings on Cassiopeia: